Уравнение времени и аналемма

Солнечные часы принципиально отличаются от всех остальных инструментов измерения времени. Дело в том, что они измеряют не одинаковые промежутки времени, как это делают все остальные часы, а движение Солнца, что не одно и то же. Разница между средним временем и солнечным описывается уравнением времени и составлет около ±15 минут.

Отображение разницы между солнечным временем и средним является крайне сложной задачей (и предметом гордости) для любого часовщика. На фото слева изображены механические часы Notos Мартина Брауна, которые помимо даты отображают значение уравнения времени и долготу Солнца.

Среднее время и фантомное Солнце

Все часы кроме солнечных отмеряют одинаковые промежутки времени и показывают среднее время. Промежутками могут быть часы, минуты, секунды или миллисекунды. Чем меньше разница между двумя одинаковыми отмеренными промежутками, тем часы точнее и, стало быть, лучше. Если бы Солнце уподобилось точным часам, то оно должно было бы вращаться вокруг Земли с постоянной скоростью по круговой орбите, расположенной в плоскости экватора. В последующих рассуждениях такое Солнце будет называться фантомным и обозначаться на чертежах серым цветом и буквой f. Все наши современные представления о времени и сама система его подсчета основаны на движении этого самого фантомного Солнца, которое обращается вокруг Земли с постоянной скоростью 24 часа в сутки. И происходит это каждый день в течение всего года. Однако в реальности орбита, по которой Солнце вращается вокруг Земли, эллиптическая, а не круговая. К тому же ось вращения Земли наклонена к плоскости вращения Солнца (эклиптике) под углом около 23,5°. Именно эти два фактора приводят к тому, что реальное Солнце t ведет себя по-другому и, наряду с фантомным средним временем, существует истинное время, которое умеют показывать только солнечные часы.

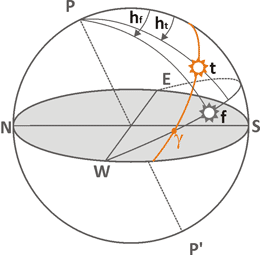
На рисунке, приведенном выше, обозначены два положения Солнца, соответствующие одному моменту времени. Фантомное Солнце f всегда движется по экватору с постоянной скоростью. Среднее местное время, которое соответствует его положению, определяется углом h_f, который откладывается от направления на юг, то есть полудня. В тоже время реальное Солнце t движется по эклиптике, которая пересекает экватор только в дни равноденствия. На рисунке эклиптика и реальное Солнце обозначены оранжевым цветом, а точка весеннего равноденствия буквой γ. Истинное время соответствует углу h_t. В общем случае эти углы не совпадают, и уравнение времени можно записать, как h_t - h_f. Описанное несоответствие среднего времени истинному имеет 6-месячный период и равняется нулю четыре раза в год: в дни равноденствия и солнцестояния. За счет фактора несоответствия эклиптики экватору (то есть из-за наклона земной оси) уравнение времени изменяется примерно от -9,87 до +9,87 минут в течение года.

Эллиптическая орбита и законы Кеплера

Вторая причина несоответствия среднего времени истинному, то есть уравнения времени, заключается в том, что годовое движение Солнца вокруг Земли происходит по эллиптической, а не круговой орбите.

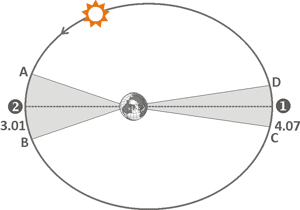
В начале XVII века немецкий астроном Иоганн Кеплер открыл три закона вращения планет, из которых к уравнению времени имеют отношение первые два. Первый закон описывает все возможные орбиты движения небесных тел относительно друг друга. В частности, при огибании Солнцем Земли по эллиптической орбите Земля располагается в одном из фокусов данного эллипса, как изображено на рисунке слева. При этом точка 1 соответствует максимальному удалению Солнца от Земли и называется апогей. Минимальное расстояние между Землей и Солнцем достигается в точке 2, называемой перигей. Ближе всего Солнце подходит к Земле 3 января, а дальше всего находится 4 июля.

Конечно, Солнце находится в одном из фокусов эллиптической орбиты, по которой Земля вращается вокруг него, но с точки зрения гномоники этот факт лишь затрудняет понимание принципов работы солнечных часов. Для тех, кто предпочитает рассматривать вращение Земли вокруг Солнца, следует заметить, что ближайшая к Солнцу точка называется перигелий, а самая удаленная - афелий.

Второй закон Кеплера утверждает, что при движении Солнца по эллиптической орбите его скорость не будет постоянной, а будет увеличиваться при приближении к Земле в точке перигея и уменьшаться в точке апогея. Саму зависимость можно проиллюстрировать графически. Солнце проходит участки AB и CD за одно и то же время в том случае, если площади соответствующих затемненных участков равны.

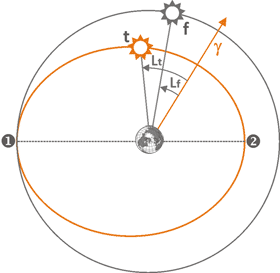
На рисунке слева изображены положения двух Солнцев: фантомного f и истинного t. Фантомное Солнце, определяющее среднее время, двигается вокруг Земли по круговой орбите с постоянной скоростью. Реальное Солнце, напротив, ускоряется возле точки перигея 2 и замедляется в апогее 1. Соответственно, долгота фантомного и реального Солнца, которая выражается углом, отложенным от точки весеннего равноденствия γ, будет разной. Доля данного несоответствия среднего времени истинному в уравнении времени выражается формулой L_t - L_f. Дважды в год, в апогее и перигее, эта разница становится равной нулю, а в остальное время она изменяется от -7,66 до +7,66 минут.

На приведенных рисунках эллиптичность орбиты намеренно подчеркнута, хотя на самом деле эксцентриситет земной орбиты составляет всего лишь 0, 017. Это означает, что орбита почти совпадает с окружностью, у которой эксцентриситет равен 0. Однако, это "почти" вносит серьезные изменения в скорость движения Солнца по эклиптике. В январе его скорость составляет 1°01' за 24 часа против 0°57' в июле.

График уравнения времени

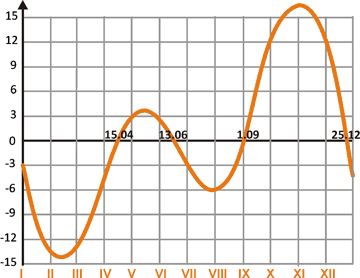
Таким образом, уравнение времени в основном складывается из двух несоответствий между временем средним и истинным, то есть солнечным. Первое несоответствие связано с наклоном земной оси. А второе несоответствие проистекает из того, что Солнце движется не по круговой, а по эллиптической орбите. Поскольку сами несоответствия сложно синхронизированы и имеют разные значения, то результирующий график уравнения времени, изображенный на рисунке в начале, несимметричен относительно нулевого значения. Уравнение времени принимает положительное значение, когда Солнце пересекает локальный меридиан раньше, чем это сделало бы фантомное Солнце, двигающееся равномерно по среднему времени. Отрицательное значение означает, что истинное время опаздывает по сравнению со средним. Как видно на графике значение уравнения времени равно нулю четыре раза в год: 15 апреля, 13 июня, 1 сентября и 25 декабря. Иногда график уравнения времени рисуют инвертированным и уравнение времени представляется, как среднее время минус истинное.

Вообще-то несоответствий между Солнцем фантомным и реальным значительно больше (известный популиризатор астрономии Фламарион описал еще 13 сложных движений Земли), но основной и заметный вклад в уравнение времени связан с орбитой Земли и наклоном оси ее вращения .

Аналемматическая кривая

Иногда уравнение времени изображают в виде аналемматической "восьмерки". В интернете можно найти фотографии, подобные размещенной. Если установить фотоаппарат на штатив и производить мультиэкспозиционную съемку каждый день в одно и тоже гражданское время, то Солнце в течение года опишет фигуру, которая похожа на восьмерку. Именно такую фигуру называют аналеммой. В зависимости от места и времени съемки кривая может иметь разную форму и наклон. Например, если бы съемка велась в 12:00 в Гринвиче, то аналемма располагалась бы строго вертикально.

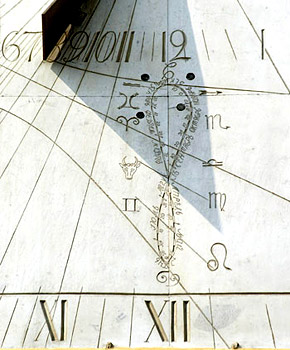
Иногда на солнечных часах изображают аналемматическую восьмерку, которая позволяет согласовать среднее и истинное время. Для этого надо знать, что полдень по среднему времени наступает, когда тень от конца гномона пересекает соответствующую часть аналеммы. Одновременно по этой тени можно определить время года, как это предполагается на часах МГУ на фотографии.

Если делаются солнечные часы, которые показывают точное среднее время, то при их разметке следует учитывать уравнение времени. Поэтому часовые линии на таких часах всегда будут в виде аналемматических кривых. Другой способ отображения среднего времени солнечными часами запечатлен на фотографии. Армилярная полусфера имеет необычный гномон в виде прорезанной аналемматической восьмерки. На изогнутой шкале представлены два времени: гражданское среднее сверху и истинное солнечное снизу.