Sun's movement
Since the times of Copernicus, it is not correct to talk about Sun's movement, as it is the Earth that rotates around the Sun, but 500 years ago it was a dangerous heresy. Moreover, if we associate a coordinate system with sundials, a primeval Ptolemy's view on our Solar system will be absolutely perfect.
Firmament
The term firmament (or celestial sphere) means a maginary sphere, with the observer in the center. The center of coordinate system, which is used in astronomy to describe the position of the objects in the sky is point O. In order to definitely describe any object, we need to know two angles: α and h.
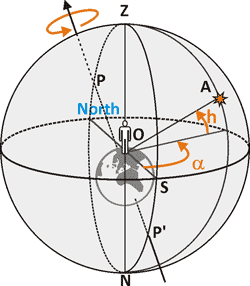
The plane of the visible horizon divides the celestial sphere into two parts: upper visible and lower invisible. The angle of elevation above the horizon h of a celestial body A is called the height. It is equal to zero when the object lies on the horizon and is equal to 90°, when it is directly overhead of the observer. This highest point Z is called Zenith. The opposite point below observer N is called Nadir.
It is naturally enough to use horizon for height measurements, but it is more difficult with an angle α. We need to postpone it from some constant direction. Points P and P' stay still while firmament's rotation. They are known as Northern and Southern Poles respectively. These are the places where Earth's axis "pierces" the celestial sphere. The closest to the point P star is called Polar. The projection Earth's axis on horizontal plane sets up a cardinal North-South direction. The angle α is called azimuth. In gnomonics it is common to measure azimuth α from the South direction OS, where Sun culminates. The change of Sun's height during the day allows to define North-South direction. Here is a simple method used since ancient times.
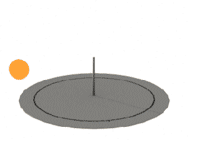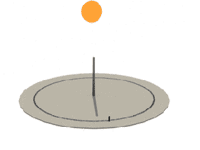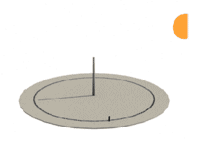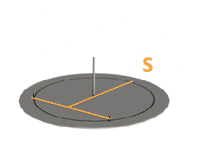
Twice a day the Sun will be at the same height, thus, the length of gnomon's shadow will be the same. Marking these moments on the circle around vertical gnomon, we can determine South direction very precisely.
The value of radius of the firmament doesn't matter, as we measure only angles to know the distance between two objects. There may be billions of light years between two celestial bodies, and 0° on the firmament, if they are visible in the same position.
Ecliptic and Zodiac
The daily movement of the Sun is the revolution of the Earth around its axis. If we look at the Earth from the Northern Pole, this rotation will be counterclockwise. In the Northern hemisphere the Sun moves across the sky from left to right (clockwise), and on the contrary in South hemishere. In addition to the daily Sun's movement, it makes the annual turnover, which is called tropical year. The duration of the tropical year (365,2422 day) makes the basis of our Grigorian calendar. The annual path of the Sun across the celestial sphere is called Ecliptic.
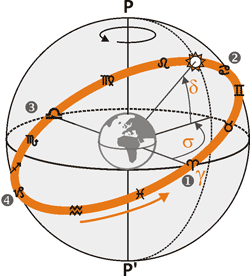
If you place the celestial sphere so that the North Pole P coincids with Zenith, the plane of the Earth's equator will coincide with the plane of the horizon, and the Ecliptic will be a path, indicated in orange. Ecliptic's plane crosses equator's plane at angle 23°27' which is equal to the angle of tilt of the earth's axis. The beginning of astronomical solar year falls on the vernal equinox, which is usually denoted by the letter γ. The vernal equinox corresponds to the Sun crossing the celestial equator at its transition from Southern hemisphere to the Northern. As can be seen in the figure after vernal equinox (point 1) the Sun moves up and reaches maximum height at point 2, which corresponds to summer solstice. Then it falls, and in point 3 reaches the autumnal equinox, where the Ecliptic intersects the plane of the equator again. Point 4 corresponds to the winter solstice. The altitude of the Sun moving along the Ecliptic, is called declination and traditionally denoted by the Greek letter δ. When the Sun is below the plane of the equator, its declination is indicated by a negative value.
At the Pole Sun's height and declanation are equal. General formula at true noon
is following:
h = 90° - φ + δ,
where h - Sun's height, φ - latitude, and δ - Sun's declination.
At the other day time the ralation is much more complex:
sin(h) = sin(δ)sin(φ) + cos(φ)cos(δ)cos(H),
where H is sun time in angular units, at true noon Н = 0°.
The term longitude is used to describe the annual position of the Sun on Ecliptics. It is an angular distance of the Sun from the vernal point γ. Longitude is marked σ, and it varies from 0° to 360°. It increments by approximately one degree (360/365.25) per day. Below is a zodiacal Sun's calendar, which is used in gnomonics.
Zodiac calendar
| Zodiac signs | Sign starts | Days | Season | |||
| Name | Sign | Date | Declination (δ) | Lonitude (σ) | ||
| Aries | ♈ | 20.03 | 00°00'00" | 0° | 30,5 | 92,8 (spring) |
| Taurus | ♉ | 20.04 | 11°28'30" | 30° | 31 | |
| Gemini | ♊ | 21.05 | 20°09'18" | 60° | 31,3 | |
| Cancer | ♋ | 21.06 | 23°26'36" | 90° | 31,5 | 93,7 (summer) |
| Leo | ♌ | 23.07 | 20°09'18" | 120° | 31,3 | |
| Virgin | ♍ | 23.08 | 11°28'30" | 150° | 30,9 | |
| Libra | ♎ | 23.09 | 00°00'00" | 180° | 30,4 | 89,8 (autumn) |
| Scorpio | ♏ | 23.10 | -11°28'30" | 210° | 29,9 | |
| Стрелец | ♐ | 22.11 | -20°09'18" | 240° | 29,5 | |
| Capricorn | ♑ | 21.12 | -23°26'36" | 270° | 29,4 | 89,0 (winter) |
| Aquarius | ♒ | 20.01 | -20°09'18" | 300° | 29,6 | |
| Pisces | ♓ | 18.02 | -11°28'30" | 330° | 30 | |
The Zodiac is a symbolic system adopted in gnomonics and astrology, unlike the zodiacal constellations, which are quite real and do not divide the Ecliptic into equal parts by 30 degrees. the Ecliptic passes through the constellation Ophiuchus, which is absent in symbolic Zodiac. Finally, the point of vernal equinox γ, which moves due to the precession, is now in the constellation of Aquarius, not Aries. However, the beginning of Zodiac year is Aries.