Analemma and equation of time

One thing makes sundials absolutely different from all other clocks: they are based on very complex movement of the Earth in the space. Although this movement has a lot of regularities (like day-night and annual seasons), it is very complex and can not be expressed in one formula. The difference between true and mean time is called equation of time (EOT). Its value varies within ±15 minutes.

The inverse problem of showing true time by mechanical clocks is considered to be one of the most complex watch complications. On the left picture you can see Notos model of Martin Braun's watches with indication of the date, EOT and Sun's declination.

Mean time and phantom Sun

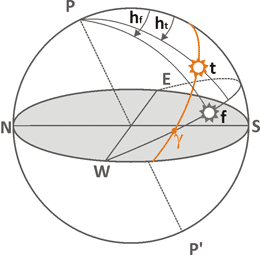
If we imagine an "ideal" Sun moving in accordance with our mean time, it would have to revolve around the Earth with constant speed in a circular orbit, located in the plane of the equator. We may call such Sun phantom, and mark it with gray color and letter f on the following drafts. All our mordern clocks are based on the constant speed of such phantom Sun.
However, the real orbit of Sun is elliptical and it is inclined to equatorial plane at an angle of about 23.5°. These two factors make the real Sun (t) to behave differently. This real movement of the Sun defines local Sun time.

There are two Sun's trajectories shown on the above draft. Phantom Sun f always moves in equatorial plane with constant speed 24 hours per turnover. Local mean time is defined by angle h_f, delayed from the South direction. Local Sun time corresponds to angle h_t. In general, these angles are not the same, and the equation of time can be recorded as h_t - h_f. Such mismatch between mean and sun time has a 6-month period and equals to zero four times a year: in the days of equinox and solstice. During the year the Earth's axis tilt contributes to the equation of time the value of ±9.9 minutes.

Elliptical orbit and Kepler's laws

The second essential component of the equation of time is an elliptical orbit of real Sun.

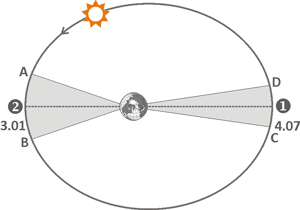
In the early XVII century a German astronomer Johannes Kepler has discovered the three laws of planetary rotation. The first two of them are relevant to origin of EOT.
The first law describes all possible orbits of the motion of celestial bodies relative to each other. According to it, the Earth is located in one of the foci of the Sun's elliptical orbit, as shown in the figure on the left. Point 1 corresponds to the maximum removal of the Sun from the Earth and is called the apogee. The minimum distance between the Earth and the Sun is reached at the point 2. Such position is called perigee. Annual perigee happens on January 3, while apogee occurs on 4 June.

For those who prefer to consider the rotation of the Earth around the Sun, it should be noted that the closest to the Sun point of the Earth's orbit is called the perihelion, and the most distant point - aphelion.

The second law states that the speed of the Sun on elliptical orbit will not be constant, but will increase when approaching perigee and decrease at the point of apogee. The dependence can be illustrated graphically. Sun passes areas of AB and CD for one and the same time, if areas of the relevant shaded sections are equal.

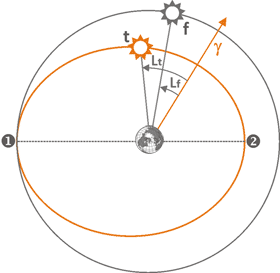
The figure on the left shows the positions of phantom Sun(f) and true Sun (t). Phantom Sun that determines mean time moves around the Earth in a circular orbit with constant speed. The real Sun, on the contrary, accelerates at perigee point 2 and slows down at apogee 1. Accordingly, phantom and real longitudes will be different. This difference is expressed by the formula L_t - L_f. Twice a year, at apogee and perigee, the difference becomes zero. The rest of the time it changes within ±7.7 minutes.

The graph of EOT

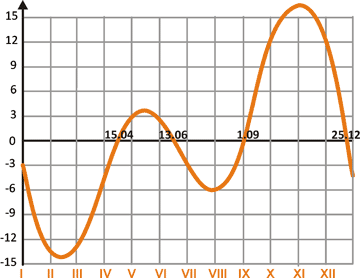
The resulting graph of the equation of time is a composition of two factors described above: Earth's axis tilt and ecliptical Earth's orbit. Equation of time takes on a positive value when real Sun crosses the local meridian before it would make a phantom Sun. A negative value means that the real Sun is late compared to phantom Sun, e.g. mean time. The value of EOT is zero four times a year: on 15th of April, 13th of June, 1st of September and 25th of December.
In some books a graphical image of the equation of time is inverted. In this case EOT is expressed as mean time minus true.

Analemmatic curve

Sometimes the equation of time is depicted in the form "analemmatic eight". In the Internet you can find pictures similar to the photo. If you set the camera on a tripod and make multiexposition shooting every day at the same mean time during the whole year, the Sun will form the shape which is similar to digit eight. Such 8-like figure is called analemma. Depending on the place and shooting time the curve can have a different shape and slope.

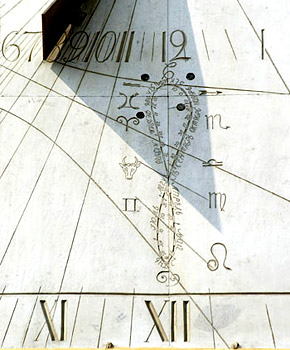
Sometimes an analemmatic curve is drawn on the dial at noon hour mark. Near noon time such curve helps to know the equation of time at certain day of the year.

If one wants to make sundials showing mean time, he has to take EOT into consideration. Therefore, the hour-lines of such sundials will always be in the form of analemma curves. Another method to display mean time by sundials is shown on the photo. The usual equatorial sundials have a gnomon in the form of a slotted analemma eight. On the curved dial two times are presented: civil time on the top, and local sun time at the bottom scale.