Basics of analemmatic sundials

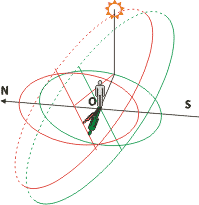
There are a lot of programs and info in the Internet, helping to construct analemmatic sundials. Just google "analemmatic sundials", and you'll find a lot of information. Here we suggest only basic formulas and simple explanations.

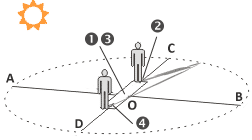
The dial of analemmatic sundials is mostly horizontal, and usually has a shape of ellipse. Hour marks are located on the border of the elliptical dial. Major semiaxis OA and minor semiaxis OC are connected by latitude-dependent relation (φ stands for latitude):

OC = OA×sin(φ)

At equator (φ = 0°, thus OC = 0) the shape of the dial becomes a line, parallel to East-West direction. On the other hand, at the Pole (φ = 90°) we get OC = OA, and analemmatic sundials become a simple equatorial sundials with a circular dial.

A yearly calendar scale is located in the center (marked О) along the Meridian line. Marks 1 and 3 correspond to equinox days, while points 2 (summer) and 4 (winter) match solstice days. When standing (or putting a vertical stick) at appropriate place on the scale, one can know sun time by observing his own shadow (or shadow from a vertical gnomon). In case of sunny day a vertical object will cast a shadow in the direction of hour marks.
If we consider major semiaxis (OA) equals 1, the dayly shift (L) on the calendar scale from the center poin 0 may be calculated as follows:

L = tg(δ)×cos(φ)

In above formula δ means Sun's declination at a given day. Keep in mind, that we can't know the exact value of the declination because of slight irragularity of our civil calendar, which depends on leap year. But existing algorithms and ephemeris tables give more-than-enough approximation.
Calendar scale may be marked as you like, but two basic methods prevail:
1) our Gregorian civil calendar is widely used and well known to everyone;
2) a symmetric division of the year, based on Sun's longitude, is known as Zodiacal calendar;

EXAMPLE
A distance of summer solstice (δ=23,5°) point 2 from center point O for Moscow latitude is:

L = tg(23,5°)×cos(56°)
L = 0,24

Thus, if we plan ОА to be equal to 2 meters, the distance between points 1 and 2 should be 48 centimeters. A total length of calendar scale in this case will be 96 centimeters.

Hour marks are always placed strictly on the constructed ellipse. If we assume some time mark to be an intersection of ellipse with a line, going from point О at an angle of α degrees, the following formula may be used:

tg(α) = tg(HA)/sin(φ)

wherе φ is latitude and HA means sun local time in degrees. Such conversion is based on the speed of the Earth's rotation - 1 hour equals 15°.

Analemmatic sundials can serve as a compass, when being combined with horizontal sundials on one base. You only need to know the date to put a vertical gnomon at the proper place. After that you should twist the base in horizontal plane until the testimonies of two sundials will coincide.
Voi la! A meridian (noon) line on the base will show North-South direction.

There are Foster-Lambert sundials, which are also considered to be analemmatic - principles of such sundials are the same as explained above. The two differences are: 1) dial's shape is always a circle and hour marks are equiangular, 2) a movable gnomon is not vertical, but stands at an angle of (90°+φ)/2.
Foster-Lambert sundials are less common probably because it is hardly possible for a sober man to stand at such an angle, unless he is not at the Pole.